Cross-Silo FL

In the cross-silo scenario where several departments or companies that own a large amount of data and computation resources want to jointly train a global model, vertical federated learning is a widespread learning paradigm. Vertical federated learning refers to the scenario where participants share the same sample ID scape but different feature spaces. For example, several companies want to federal learn global user profiles with their app data, which have a large amount of overlapped users but different user behaviors.

Settings

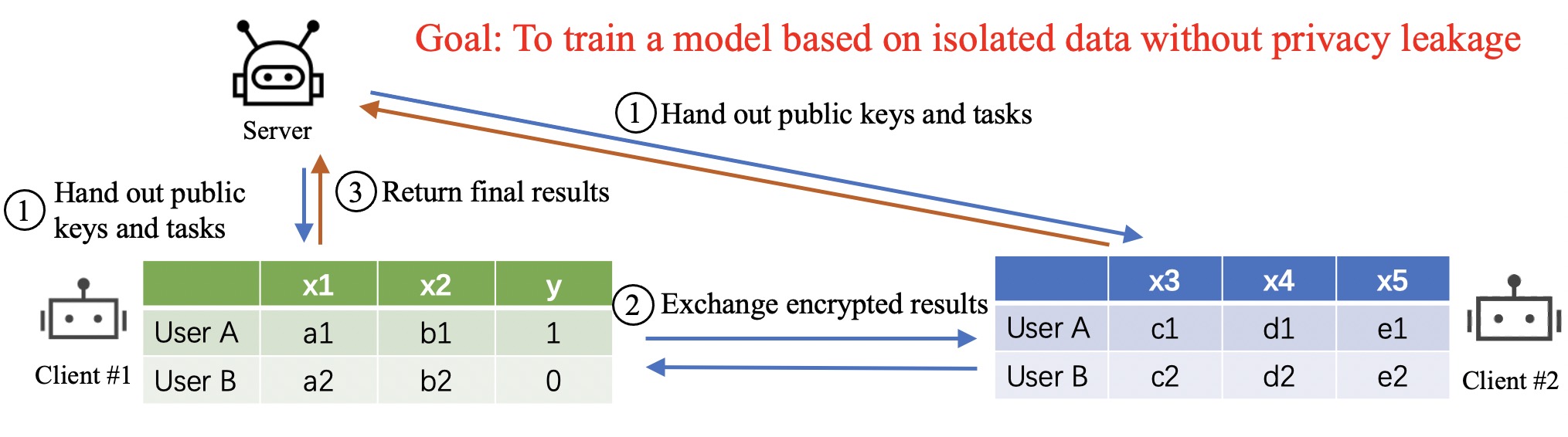A typical process of Vertical FL is illustrated in the figure. Clients own different features within $(x1,x2,x3,x4,x5)$ and one of them owns the labels$y$. After aligning the user ID space via a private set intersection, participants aim to train a model based on the isolated data without directly sharing the features. The general process includes:

  1. A server (also called a coordinator) hands out public keys (for encrypting the results) and computation tasks to clients;
  2. Each client computes a part of the results based on the data, encrypts them, and exchanges the encrypted results with each other;
  3. Then each client finishes the computation task and returns the final results to the server;
  4. The server aggregates the results and updates the model.

Note that in the vertical FL, homomorphic encryption techniques might be used to make sure the correctness of the computation while protecting privacy.

Next we will introduce an example and show how to implement it with FederatedScope.

Example and implementation

We task the study from [1] as an example. To be simplified, we focus on the secure logistic regression (Algorithm 2 in the paper) while ignoring the entity matching process. Before introducing the algorithm, we need to present the additively homomorphic encryption and Taylor approximation for the objective function first.

Additively homomorphic encryption: Paillier

Paillier [2] is used to make sure the correctness of the computation while protecting privacy. We use the following notations for Paillier:

  • $[\cdot]$ denotes the encryption
  • Due to the characteristics of additively homomorphic encryption, we have$[u] + [v] = [u+v]$and $v[u] =[vu]$

Note that Paillier can be extended to the inner product or element-wise product.

Taylor approximation for the objective function of LR

The objective function of logistic regression is not suitable to be calculated via additively homomorphic encryption, thus we need to perform the Taylor approximation according to [1]. Specifically,

  • Given the training set $S = {(x_i,y_i)_{i=1}^n}$, with logistic regression, we learn a linear model $\theta\in \mathbb{R}^d$ that maps $x\in \mathbb{R}^d$ to binary labels $y\in{-1,1}$.
  • The loss can be given as $L_S(\theta) = \frac{1}{n}\sum_{(x_i,y_i)\in S} \log(1+e^{-y_i\theta^{\top}x_i})$
  • With the Taylor series expansion of $\log(1+e^{-z})$ around $z=0$, the second-order approximation of the loss is$L_S(\theta) \approx \frac{1}{n}\sum_{(x_i,y_i)\in S}\left( \log 2 - \frac{1}{2}y_i {\theta^{\top}x_i}+\frac{1}{8}(\theta^\top x_i)^2 \right)$
  • The gradient can be given as $\nabla L_{S}(\theta) \approx \frac{1}{n}\sum_{(x_i,y_i)\in S}\left( \frac{1}{4}\theta^\top x_i - \frac{1}{2}y_i \right)x_i$

Algorithm

Then we can describe the algorithm in [1] via message passing. Suppose that there exist two participants, A and B, which own the same number of instances$n$. And only A has the labels$Y$. We denote the features as$X = [X_A X_B]$, $X\in \mathbb{R}^{n\times d}$. There also exists a Coordinator C (i.e., the server).

We can decompose $\theta^\top x =\theta_A^\top x_A+\theta_B^\top x_B$. The algorithm via message passing can be summarized as:

  • Coordinator C:
    • Send$\theta$to A, B;
    • Send public keys to A, B;
  • participant A:
    • Sample a batch of data with indexes$S’$ ;
    • Compute $u_A = \frac{1}{4}X_{A,S’}\theta_A - \frac{1}{2}Y_{S’}$ and encrypt (via Paillier): $[u_A]$;
    • Send$S’$ and $[u_A]$ to B;
  • participant B:
    • Compute $u_B = \frac{1}{4} X_{B,S’}\theta_B$ and encrypt (via Paillier): $[u_B]$ ;
    • Compute $[u] = [u_A] + [u_B]$ ;
    • Compute $[v_B]=X_{B,S’}[u]$ ;
    • Send $[u]$ and $[v_B]$ to A ;
  • participant A:
    • Compute $[v_A]=X_{A,S’}[u]$ ;
    • Send $[v_A]$ and $[v_B]$ to C ;
  • Coordinator C:
    • Obtain $[v]$ by concatenating $[v_A]$ and $[v_B]$ ;
    • Decrypt to obtain the gradients $v$ ;

To implement the algorithm in FederatedScope, developers need to abstract the types of exchanged messages and transform the behaviors into handling functions. For example:

# For Coordinator C
Received messages: 
  [v_a] & [v_b]
Handling functions:
  when receiving [v_a] & [v_b] -> concatenates [v_a] & [v_b], and decrypt; 

# For Participant A
Received messages: 
  theta & public_key, [u] & [v_b]
Handling functions:
  when receiving theta & public_key -> sample a batch of data, compute [u_a], send sampled indexes and results to participant B;
  when receiving [u] & [v_b] -> compute [v_a], send [v_a] & [v_b] to Coordinator C;

# For Paritcipant B
Received messages:
  theta & public_key, S' & [u_a]
Handling functions:
  when receiving theta & public_key -> wait for intermediate results from participant A;
  when receiving S' & [u_a] -> compute [u] and [v_b], send [u] & [v_b] to participant A;

Users can refer to New types of messages and handlers for more details about how to add new types of messages and handlers to customize an FL task.

References

[1] Hardy S, Henecka W, Ivey-Law H, et al. “Private federated learning on vertically partitioned data via entity resolution and additively homomorphic encryption”. arXiv preprint, 2017.
[2] Paillier P. “Public-key cryptosystems based on composite degree residuosity classes.” International conference on the theory and applications of cryptographic techniques. 1999: 223-238.

Updated: